필자는 수학을 못한다. 학생 시절 시험을 치면 다른 과목에서는 하나, 많이 틀리면 두개 정도 틀렸지만 수학만큼은 하나 아니면 두개 정도 맞을 정도로 수학에 대해서는 잼병이다. 본 포스트는 수학을 못하는 필자가 어떻게 삼각함수를 이해하게 되는지에 대한 과정을 그리고 있다.
정의
삼각함수의 정의로 서론을 시작하고 싶었지만, 머릿글에 언급 했듯이 필자는 수학 잼병이라 위키에 소개된 삼각함수의 정의를 봐도 무슨 말인지 이해를 못했다 :
https://ko.wikipedia.org/wiki/%EC%82%BC%EA%B0%81%ED%95%A8%EC%88%98
라디안
나에게는 항상 낮설고 불편하지만, 삼각함수에서 꼭 빠지지 않고 나오는 '라디안'. 우리가 일반적으로 사용하는 60분법을 사용하면 익숙하고 편할 것 같은데 삼각함수는 항상 이 '라디안'이라는 것을 이용해 계산을 한다. 이번 장에서는 라디안을 60분법으로 변경하는 방법, 그리고 그 반대의 방법을 알아 보겠다.
'라디안(rad)'의 정의 :
원에서 반지름의 길이와 같은 길이를 갖는 호에 대응하는 중심각의 크기
여기서 '원', '반지름', '호'와 같은 기본적인 단어들에 대한 설명은 하지 않겠다(이 글을 읽는 여러분은 이 단어들의 의미를 이미 알고 있다고 믿는다). 하나의 원을 아래 그림 처럼 피자 조각 모양으로 잘랐을 때, 반지름의 길이와 호의 길이가 같을 때의 각을 1라디안(rad) 라고 한다.
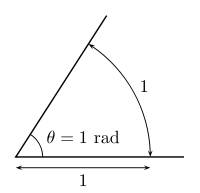
θ - 세타라고 읽으며, 수학에서 미지의 각도를 나타낼때 쓰인다(https://ko.wikipedia.org/wiki/%CE%98)
사실 정의를 보고도 무슨 소리인지 잘 이해가 가지 않는다. 그래서 1라디안(rad)이 몇 도란 말인가? 그것을 알아 보기 위해 일단 원주(원의 둘레의 길이)를 구하는 공식을 살펴 보자.
원의 둘레 길이를 구하는 공식은 2 * 반지름 * 3.14다. 좀 더 수학적으로 써보면 2πr 이다. 그럼 반지름만큼의 각 1rad는 원의 전체의 각 360°와 원주 전체의 길이 2πr을 가지고 360° : 2πr = 1rad : r 라는 비례식을 얻을 수 있다.
비례식을 풀면 360° * r = 2πr * 1rad, 이항을 해서 1rad = 360° * r / 2πr.
이것을 약분 하면 1rad = 180° / π 를 얻을 수 있다.
(※ 나 처럼 비례식을 풀 줄 모른다면 여기로 -> mathbang.net/326)
1 rad = 180°/ π
아래와 같이 이항해서 1°가 몇 라디안인지 구할 수 있다.
1rad * π / 180° = 1°
360°는 어떨까? 간단히 양변에 360을 곱해주면 위와 같은 공식을 얻을 수 있다.
2π rad = 360°
삼각함수
직각삼각형은 두 변이 이루고 있는 한 각이 직각(90도)인 삼각형이다. 삼각함수의 삼각비는 이 직각삼각형의 변의 비율로 찾을 수 있다. 직각을 마주 보고 있는 빗변의 길이에 대한 높이의 길이의 비가 ‘사인(sine)’이다. 빗변의 길이에 대한 밑변의 길이의 비는 ‘코사인(cosine)’이다. 밑변의 길이에 대한 높이의 길이 비를 ‘탄젠트(tangent)’라 한다. 직각삼각형의 크기에 상관없이, 세 각의 크기가 같으면 사인, 코사인, 탄젠트 값은 언제나 같다.
from : https://news.samsungdisplay.com/24578/
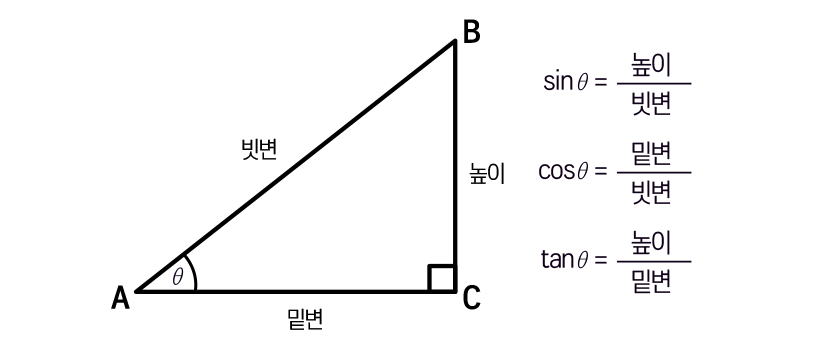
- sinθ = 높이(대변)/빗변
- cosθ = 밑변/빗변
- tanθ = 높이(대변)/밑변
위 공식이 어떻게 나왔는지 설명할 능력은 없다. 여기까지는 그냥 외우자. 좀더 쉽게 외우는 방법은 '삼각함수 공식 쉽게 외우는 방법'을 참고하자. 요약하면 :

- cos은 알파벳 C를 삼각형 위에 쓰면서 '빗변 분의 밑변(밑변/빗변)'이라고 기억하자.
- tan은 알파벳 소문자 t를 삼각형 위에 쓰면서 '밑변 분의 높이(높이/밑변)'라고 기억하자.
- sin은 알파멧 S를 삼각형 위에 쓰면서 '빗변 분의 높이(높이/빗변)'라고 기억하자.
삼각함수를 어디에 쓰나요?
이렇게 라디안, sin, cos, tan에 대해 알아 보았다. 그렇다면 도데체 이걸 어디에 쓰길래 우리는 머리 아프게 삼각함수에 대해서 공부를 해야 하는가? 삼각함수를 이해하게 된다면 두 점의 사이의 각을 알아 낼 수 있다.
예를 들어 아래 예문을 보자 :

발사 위치가 A(8, 4)에 있고, 목표물은 B(2, 1)에 있다. 발사 위치와 목표물간의 각도를 구하라.
1. 피타고라스 정리를 이용하여 발사 위치와 목표물 간의 거리를 구해보자.
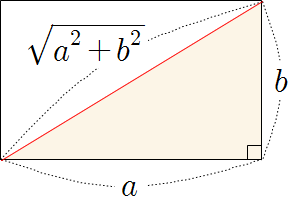
거리 D 는 √(8-2)2 + (4-1)2
= √36 + 9
= 6.7082039325
두 지점간의 거리는 6.7082039325 다.
2. 그래서 '?' 각의 크기는?
- 빗변의 길이는 6.7082039325
- 높이(대변)의 길이는 3
- 밑변의 길이는 6
피타고라스 정리를 이용하여 빗변의 길이 까지 구하면 각 삼각형 변의 길이는 위와 같다. 직각 삼각형에서 각변의 길이를 알고 있으니 이제 삼각함수를 이용하여 각을 알아 낼수 있다. 물음표가 있는 꼭지점의 각, cosθ는 밑변/빗변(6/6.7082039325). 즉, 0.894427191다.
cos 함수에 알 수 없는 미지의 값 θ를 넣었더니 그 결과가 0.894427191라고 한다. 그럼 저 0.894427191를 나오게한 미지의 값 θ는 어떻게 구할까? 그 값을 구하기 위해 역코사인 함수(arccos) 라는 도구가 존재 한다 :
cos-1(θ)
공학용 계산기를 이용해 역함수를 실행하면 cos-1(0.894427191) = 0.4636476090 rad 또는 26.565051177° 이 나온다.
※ 라디안 값과 60분법을 모두 언급한 이유는, 공학용 계산기에는 삼각함수를 60분법(Degree)로 계산 할지 라디안(Radian)으로 계산 할지 선택 할 수 있는 옵션이 있다. 필자는 그걸 몰라 값이 자꾸 이상하게 나온다고 한참을 헤매었다.
[도구의발견] - 윈도우 공학용 계산기로 삼각함수 구하기
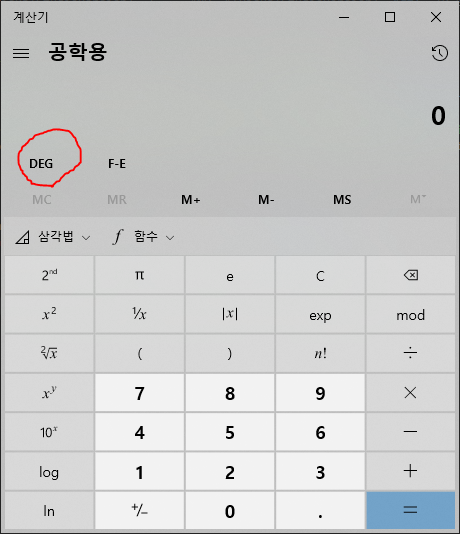
이번에는 라디안 결과 값에서 60분법 각으로 변환 시켜 보자. 위 라디안의 정의에서 2π = 360이라는 것을 알게 되었다. 그럼 이것을 이용하여 비례식을 만들어 보자.
2π : 360 = 0.463647609 : x
비례식을 풀어 보면 360 * 0.463647609 = 2πx 를 얻을 수 있다. x를 구하기 위해 2π를 왼쪽으로 이항하고 약분 하면, 180 * 0.463647609 / π = x
즉, x = 26.565051177 다.
부록1. 참고
- 삼각 함수 정의 : ko.wikipedia.org/wiki/%EC%82%BC%EA%B0%81%ED%95%A8%EC%88%98%EF%BB%BF
- 세타 정의 : ko.wikipedia.org/wiki/%CE%98dsfsd
- 비례식 풀이 방법 : mathbang.net/326
- 삼각 함수 정의 2 : https://news.samsungdisplay.com/24578/
- 삼각 함수 공식 쉽게 외우는 방법 : engineershelp.tistory.com/37
- 라디안 호도법 각도 단위 변환 계산기 : mwultong.blogspot.com/2008/02/rad-radian-degree-calc.html
- 삼각 함수의 기초 : m.blog.naver.com/ohrak22/30112519627


