들어가며
필자는 픽셀 던전과 같은 던전을 탐험하는 로그라이크 게임을 좋아한다. 세상에는 이미 천재들이 만들어 놓은 명작 로그라이크 게임들이 존재하지만, 항상 나만의 스토리와 퀘스트를 가진 나만의 로그라이크 게임을 가지는 꿈을 가지고 있다.

그 시작으로 이번 포스트에서는 로그라이크 게임의 메인 요소인 '랜덤하게 생성되는 던전'에 대한 내용을 다뤄 보도록하겠다. 본 포스트에서는 랜덤 던전을 만들기 위한 기술과 알고리즘들 살펴 볼 것이며, 필자가 이 포스트를 위한 예제를 만들며 직접 겪은 경험들과 생각들 또한 더해보도록 하겠다.
본 포스트에 사용된 예제는 유니티 기반으로 개발 되었으며 전체 프로젝트는 [여기]에서 확인할 수 있다. 만일 여러분이 코드를 분석하고자 한다면 주요 알고리즘과 자료 구조는 DungeonGenerator.cs에 모두 구현 되어 있으므로 궁금하신 분들은 해당 파일을 위주로 확인하길 바란다. 나머지는 시각화와 편의를 위한 에디터 기능들이니 그리 중요하게 볼 필요는 없을 것이다.
이외에도 랜덤 던전을 만들기 위해 필요한 사전 지식으로는 :
정도가 있으나, 포스트를 진행하면서 다시 언급할 것이므로 지금 당장 여기서 볼 필요는 없다.
Procedural Dungeon Generation Algorithm
'랜덤 던전'은 영어로는 'Procedural dungeon generation', 직역하면 '절차적 생성 던전'이라고 한다. 하지만 일반적으로 '랜덤 던전', '랜덤 맵'이 더 익숙하므로 본 포스트에서는 '랜덤 던전'이라는 용어를 사용하도록 하겠다.
랜덤 던전을 만들기 위해서는 다음과 같은 과정이 필요하다.
- 적당한 크기의 방들을 적당한 위치에 배치
- 적당한 방들을 연결하여 경로 만들기
- 방과 경로를 기반으로 실제 던전 만들기
여기서 우리가 주목해야 할 부분은 '적당함'이다. 만일 문자 그대로 던전을 '랜덤'하게만 생성한다면 캐릭터가 이동할 수 없거나 방들을 연결할 수 없는 결과물이 만들어질 수 있다. '적당함'을 위해서는 통제된 범위 내에서의 랜덤성이 필요하다. 이제 부터 '통제된 범위 내에서의 랜덤'을 위한 기술들에 대해 살펴 보도록 하자.
방(Room) 생성
먼저 던전의 방 생성에 관련된 랜덤의 범위를 정해보자.
- 방 크기는 지정된 최소/최대 범위 내에서 랜덤하게 결정 되어야 한다.
- 방은 영역 내에서 고르게 분포된 위치에 배치 되어야 한다. 가로 또는 세로로만 길게 일렬로 배치 되어서는 안된다.
- 방이 배치 될 때, 방 간의 거리는 0에서 부터 최대 범위 사이에서 랜덤하게 결정 되어야 한다.
방 크기
방 크기의 랜덤 범위를 지정하는 것은 매우 간단하다. 단순 랜덤 함수를 이용해 지정된 범위 내에서의 방의 가로 길이와 세로 길이를 결정하고 그에 따라 사각형을 만들면 된다.
int width = Random.Range(minRoomSize, maxRoomSize);
int height = Random.Range(minRoomSize, maxRoomSize);
Block block = new Block(width, height);다만 위와 같이 가로, 세로 길이가 독립적인 랜덤 값을 가지게 되면 아래 그림과 같이 방이라고 부르기에는 곤란한 길다란 통로 같은 방들이 생성 되는 경우가 있다. 특히 다양한 크기의 방을 생성하기 위해 최대/최소 값의 차이를 크게 주는 경우 두드러지게 발생한다.

그래서 필자의 경우 한쪽 축의 길이를 정한 뒤, 그 값에 랜덤하게 비례하도록 다른 축의 길이를 정했다. 거기에 더해 가중치 랜덤을 사용하여 특정 길이나 비율을 가진 방들이 더 많이 생성되도록 조절 했다.
int width = 0;
int height = 0;
if (0 == Random.Range(0, 100) % 2) // 50% 확류로 가로 또는 세로 기준 축을 잡음
{
width = GetWeightRandomRoomSize(minRoomSize, maxRoomSize)
height = width * GetWeightRatioOfRoomSize(0.5f, 3.0f);
height = Max(minRoomSize, height);
height = Min(maxRoomSize, height);
}
else
{
height = GetWeightRandomRoomSize(minRoomSize, maxRoomSize)
width = height * GetWeightRatioOfRoomSize(0.5f, 3.0f);
width = Max(minRoomSize, width);
width = Min(maxRoomSize, width);
}
Block block = new Block(width, height);앞의 결과와는 달리 극단적인 직사각형의 방들은 사라진것을 확인할 수 있다.

방 배치
이번 섹션은 필자가 가장 많은 시도와 실패를 했고 시간을 많이 쓴 '방 배치'에 대해 살펴 보도록 하겠다.
가장 먼저 시도 했던 방법은 Binary Space Partitioning(BSP)라고 불리는 공간을 재귀적으로 분리하고 각 공간에 방을 배치하는 방법이었다.

하지만 이 방법은 위 그림과 같이 특정 선을 기준으로 너무 인위적으로 공간이 갈라져 있는 느낌이 들어 필자가 원하는 형태는 아니었다.
BSP 말고도 여러 다른 방법들 시도해 보았지만 계속 원하는 결과를 얻지 못하다, 'TinyKeep'이라는 게임에서 사용된 랜덤 던전 알고리즘을 소개하는 흥미로운 포스트를 발견했다. Procedural Dungeon Generation Algorithm에서는 "특정 영역(일반적으로 '원' 또는 '타원') 내에 랜덤 위치의 방들을 생성하고, 만일 방들이 서로 겹친다면 각 방들을 서로 겹치지 않는 위치까지 이동"시켜 방들을 고르게 배치하는 알고리즘"에 대해 소개하고 있다.
해당 포스트에서는 실제 알고리즘 동작 방식을 시각화하여 보여주고 있는데 알고리즘의 동작방식을 한눈에 이해할 수 있을 것이다.

이 알고리즘의 핵심은 방들을 겹치지 않는 위치까지 어떻게 이동시키는가이다. 필자의 경우, 단순히 원점으로 부터 x, y 축 좌표가 증가하는 방향으로 이동시켰더니 아래 처럼 L자 형태로 방들이 배치되는 결과가 생성되었다.

Procedural Dungeon Generation Algorithm에서 처럼 방들의 위치를 이동 시키기 위해서는 사각형 그룹의 중심에서 부터 바깥 방향으로 퍼뜨리면서 방들을 이동시켜야 한다. 이것을 코드로 작성하면 아래와 같다 :
void RepositionBlocks()
{
Vector2 center = GetCenterOfBlockGroup(); // 생성된 전체 블록들의 중심을 구한다.
while (true)
{
bool overlap = false;
for (int i = 0; i < blocks.Count; i++)
{
for (int j = i + 1;j < blocks.Count; j++)
{
if (true == blocks[i].Overlaps(blocks[j]))
{
ResolveOverlap(center, blocks[i], blocks[j]);
overlap = true;
}
}
}
if (false == overlap)
{
break;
}
}
}
void ResolveOverlap(Vector2 center, Block block1, Block block2)
{
int dx = Min(Abs(block1.x+block1.width-block2.x), Abs(block2.x+block2.width-block1.x));
int dy = Min(Abs(block1.y+block1.height-block2.y), Abs(block2.y+block2.height-block1.y));
// 거리가 가까운 축 기준으로 블록 이동
if (dx < dy) // 두 블록이 x축으로 더 가까움
{
if (block1.x < block2.x) // 두 블록 중 block2가 오른쪽 있는 경우
{
if (center.x < block2.x)
{
block2.x += 1; // block2가 중앙 보다 오른쪽에 있으면 block2를 오른쪽으로 1칸 이동
}
else
{
block1.x -= 1; // block2가 중앙 보다 왼쪽에 있으면 block1을 왼쪽으로 1칸 이동
}
}
else // 두 블록 중 block1이 오른쪽 있는 경우
{
if (center.x < block1.x)
{
block1.x += 1; // block1이 중앙 보다 오른쪽에 있으면 block1를 오른쪽으로 1칸 이동
}
else
{
block2.x -= 1; // block1가 중앙 보다 왼쪽에 있으면 block2를 왼쪽으로 1칸 이동
}
}
}
else // 두 블록이 y으로 더 가까움
{
if (block1.rect.y < block2.y)
{
if (center.y < block2.y)
{
block2.y += 1; // block2가 중앙 보다 위에 있으면 block2를 윗쪽으로 1칸 이동
}
else
{
block1.y -= 1; // block2가 중앙 보다 아래에 있으면 block1을 아래로 1칸 이동
}
}
else
{
if (center.y < block1.y)
{
block1.y += 1; // block1이 중앙 보다 위에 있으면 block1을 위로 1칸 이동
}
else
{
block2.y -= 1; // block1이 중앙 보다 아래에 있으면 block2를 아래로 1칸 이동
}
}
}
}블록을 한번에 겹치는 길이만큼 움직이지 않고 1씩 이동 시킨 이유는, 한번에 이동 할 시 고르게 퍼지지 못하고 역시 L자형 던전을 만들기 때문에 1칸씩 움직이면서 다른 축으로도 움직일 기회를 주는 것이다. 위 코드는 예제로 사용하기 위해 생략 된 부분이 많으므로 오리지널 코드를 보고 싶다면 [여기]를 확인하길 바란다.
아래 그림은 위 알고리즘을 이용해 각각 10개, 30개, 50개의 방을 생성했을 때 균일하게 배치되는 방들의 위치를 보여 주고 있다.



배치는 해결 되었으니, 이제 방 간의 거리에 대해 이야기 해보자.
Procedural Dungeon Generation Algorithm에서는 수 많은 블록들을 생성 후 특정 조건에 맞는 몇 개를 선택하여 방으로 선정하고 나머지는 복도 공간으로 쓰는 방법을 소개하고 있다. 하지만 이 방법의 경우 조건에 맞는 방이 너무 적거나, 너무 많은 경우 원했던 방의 갯수와 결과물의 갯수가 큰 차이가 나는 경우가 많았고, 방 간의 거리 또한 통제가 되지 않았다.
그래서 나는 필요한 갯수 만큼의 방을 미리 생성한 후, 복도로 사용될 공간을 기존 방과 방 사이에 끼워 넣는 방법을 사용했다.
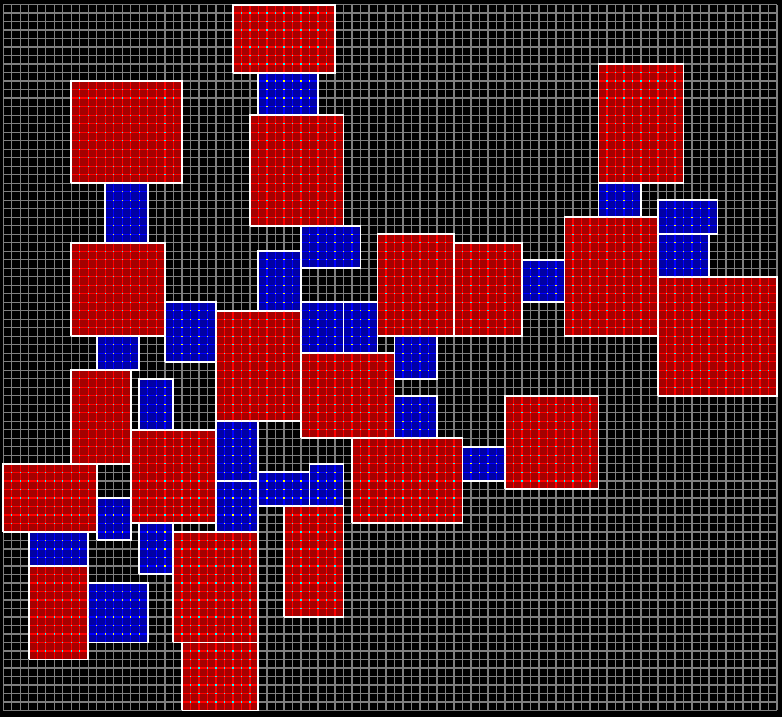
위 그림은 방과 방 사이에 새로운 블록들을 추가하여 복도 공간을 확보한 결과를 보여주고 있다. 빨간색 블록은 방, 파란색 블록은 복도를 구성하기 위해 추가된 블록들이다.
복도(Corridor) 생성
이번 섹션에서는 앞에서 만든 방들을 연결하여 통로를 구성하는 방법에 대해 살펴 보도록 하자. 던전의 방을 연결하는 통로는 다음과 같은 조건을 가진다 :
- 방은 최소 하나 이상의 다른 방과 연결 되어 있어야 한다.
- 한 방으로 부터 던전의 모든 방에 도달할 수 있음을 보장해야 한다.
위 조건에서 먼저 생각해야 할 것은 어떤 방들이 연결 되어야 하는가이다. 랜덤에만 의존해 방을 연결하게 되면 아래 그림과 같이 서로 도달하기 먼 거리의 방을 연결한다거나(빨간색 선), 서로 다른 연결 써클(하얀선과 빨간선으로 연결된 방들은 서로 연결되어 있지 않다)을 만들어 던전이 단절되는 현상이 발생할 수 있다.
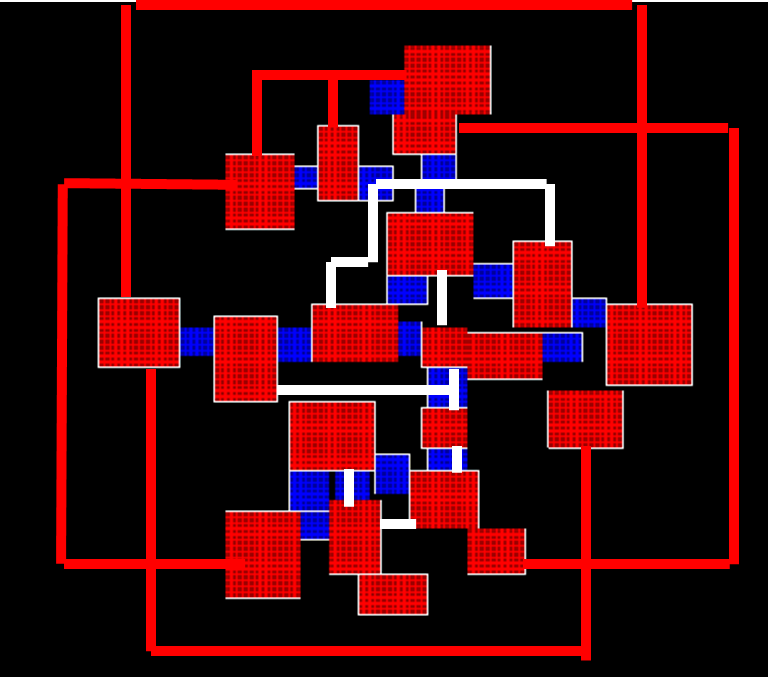
우리는 '들로네 삼각분할법(Delaunay Triangulation)'과 '최소 신장 트리(Minimum Spanning Tree)'를 이용해 위 문제를 해결할 것이다.
Delaunay Triangulation + Graph
'들로네 삼각분할(Delaunay Triangluation)'은 평면위의 각 연결 점들을 정삼각형에 가깝도록 연결하여, 연결점간 거리를 최소화하는 공간 분할 방법이다. 들로네 삼각분할을 이용하여 각 방의 중심점들을 연결하면 아래 그림과 같이 모든 방을 포함하며 인접한 방들끼리만 간선이 연결된 그래프를 얻을 수 있다.
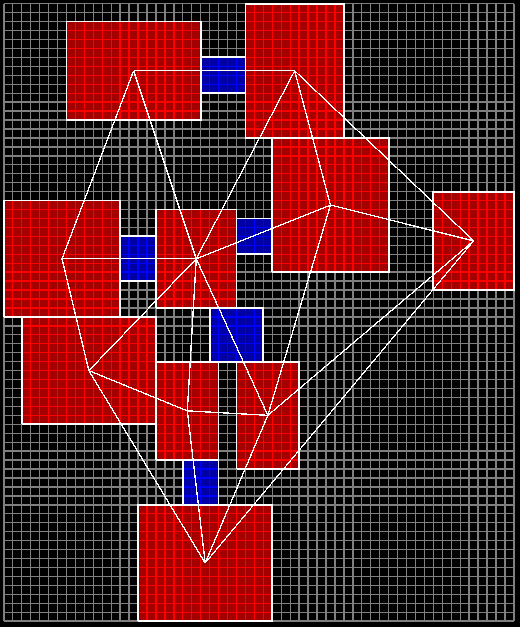
들로네 삼각분할에 대한 내용은 양이 만만치 않아 보이어 왓슨(Bowyer-Watson) 알고리즘 - 제목이 '들로네 삼각분할'이 아닌 이유는 포스트를 읽어 보시면 알게 될것이다 - 포스트에 별도로 자세히 정리해 두었다. 관련 소스 코드는 [여기]에서 간단히 확인하고 복사해서 사용할 수 있지만, 원리가 궁금하신 분은 링크된 포스트를 같이 보는 것을 추천한다.
Minimum Spanning Tree
앞서 들로네 삼각분할을 이용해 모든 방들이 연결된 그래프를 얻었다면, 이젠 실제 방을 연결하는데 사용될 간선을 선택해야 할 차례다. 이를 위해 '최소 신장 트리(Minimum Spanning Tree)' 알고리즘을 이용할 수 있다.
최소 신장 트리(Minimum Spanning Tree'는 주어진 그래프에서 일부 간선을 선택해서 만든 트리로써, 모든 정점들이 연결 되어 있어야 하고 사이클을 포함하지 않는 형태를 가지는 트리다.
'최소 신장 트리'는 던전의 모든 방에 도달할 수 있음을 보장하지만, 들로네 삼각분할의 그래프 처럼 모든 방들이 연결되지는 않도록 한다. 우리는 모든 방들끼리 연결되어 있는 것을 원하지 않지만, 그렇다고 도달할 수 없는 방이 생성되는 것도 원하지 않기 때문에 던전의 통로를 위한 간선을 결정하기에 적합한 방법이다.
그리고 경로가 하나 뿐인 던전은 탐색을 단조롭게 만들 수 있으므로, 최소 신장 트리에 의해 결정 된 경로 외에 확률에 의해 몇 개의 통로를 더 추가하여 목표 지점까지 이동할 수 있는 다양한 경로를 가질 수 있도록 했다.
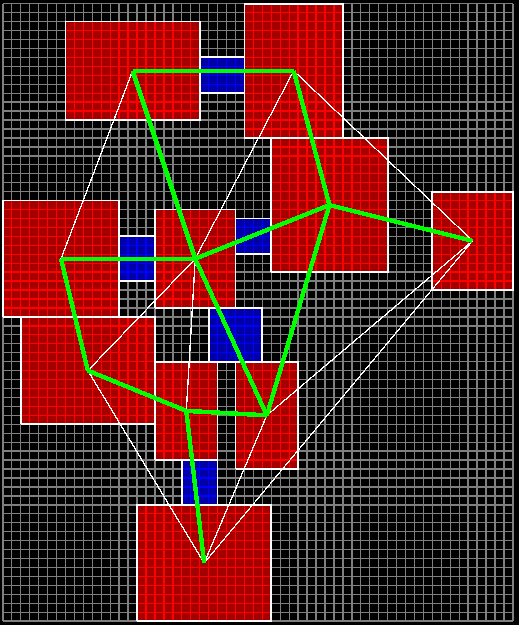
위 이미지에서 녹색으로 표현된 선들이 앞으로 복도가 될 간선들이다. 최소 신장 트리는 써클을 생성하지 않지만 추가된 경로로 인해 써클 경로가 생성된것을 볼 수 있다.
A*(star) Path Finding Algorithm
지금까지 '들로네 삼각분할'과 '최소 신장 트리'를 이용해 어떤 방들 간에 통로를 만들지 결정했다. 이제는 캐릭터가 걸어갈 실제 경로를 만들어야 할 차례이다. 본 예제에서는 연결점 간의 경로를 정하기 위해, A* 길찾기 알고리즘을 이용했다.
A* 알고리즘은 타일로 구성된 2차원 맵에서 각 타일에 이동 비용을 설정하고 이동 비용이 적은 쪽의 경로를 택하여 목적지에 도달하는 방식이다. 필자는 이것을 이용하여 각 타일에 다른 이동 비용을 할당해 경로를 필자가 원하는 대로 유도하고자 했다.
예를 들어, 아래 그림에서 검은색으로 표시된 빈 공간을 나타내는 타일은 이동 비용을 가장 높게 할당하여 경로로 선택 될 확률을 낮추고, 블록 타일(빨간색과 파란색)은 그보다 낮게, 블록타일의 가운데 부분은 더 낮은 이동 비용을 할당해 빈 공간 보다는 블록을, 블록을 지난다면 한 가운데를 경로로 선택 하도록 했다.
필자는 A* 알고리즘으로 경로를 생성하며 한가지 난감한 문제에 부딫혔었다. A* 알고리즘이 최단 경로를 찾는 알고리즘이다 보니, 이미 주변에 생성된 경로가 있는데도 불구하고 또 다른 최단 경로를 만들어 비슷한 경로들이 너무 많이 생성되어 던전이 거미집 처럼 되었다.
이을 해결하기 위해 타일이 경로로 지정될때 마다 해당 타일의 이동 비용을 점점 더 낮추는 방법을 사용했다. 이를 이용해 새로운 경로를 탐색하더라도 기존 경로가 어느 정도 가까이 있다면 절대적으로 이동 비용이 낮은 기존 경로를 선택하게 하여 위 거미집 문제를 해결 했다.
아래 그림을 자세히 보면 하얀색으로 표시된 경로 타일들의 진하기가 다른 것을 볼 수 있다. 경로가 한번 선택 될 때마다 해당 타일에 하얀색 스프라이트를 올렸기 때문에 다른 것 보다 진하다는 것은 해당 타일이 여러번 경로로 선택되었다는 것을 의미한다.
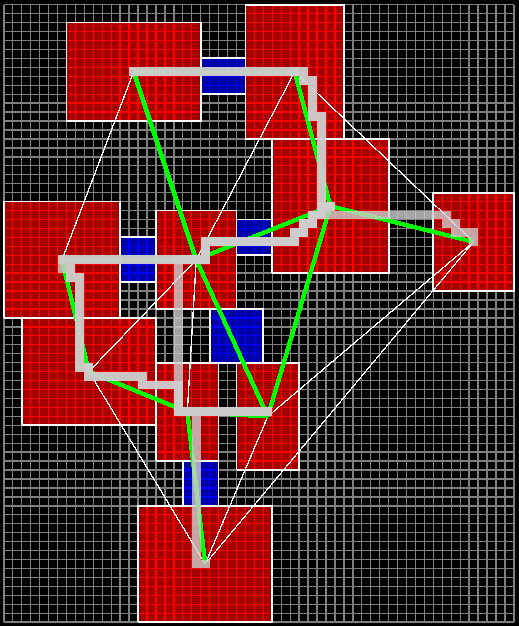
이렇게 경로의 가중치를 점점 낮추는 방법을 사용하면 아래 그림 처럼 방 블록 간의 거리가 너무 먼 경우 두 방 간의 긴 경로를 만드는 것이 아니라, 기존의 경로들을 거쳐 가는 방법으로 훨씬 자연스러운 결과를 도출 할 수 있다.
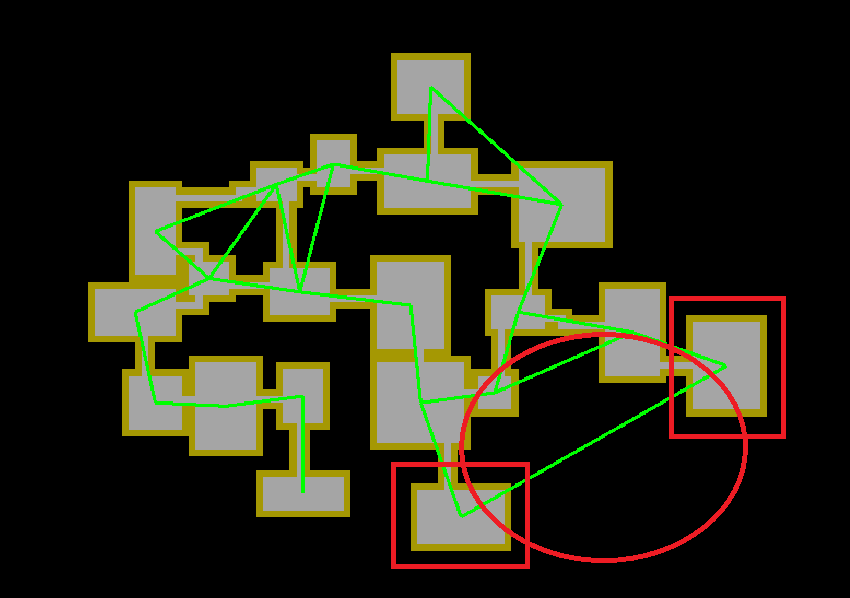
위 이미지에서 두 빨간 사각형 내의 방이 연결되어야 하나 길다란 경로를 새로 만드는 대신 기존에 만들어져 있는 경로를 이용하는 것을 볼 수 있다.
마치며
이상 랜덤 던전을 만들기 위한 모든 과정들을 끝냈다. 아래는 앞에서 얻은 타일맵 데이터를 이용해 간단하게 던전을 시각화 해본 결과물이다.

[다음 포스트]에서는 오토 타일링을 이용해 생성된 던전 데이터 위에 그래픽 요소를 추가하는 것에 대해 살펴 보도록 하겠다.
부록 1. 예제 프로젝트 사용법
본 포스트에 사용된 예제 프로젝트는 [여기]에서 찾아 볼 수 있다. 프로젝트를 다운로드 받은 후 유니티를 실행하고, 프로젝트에 포함되어 있는 'Dungeon' 씬을 실행하면 Hierachy 창에서 'Dungeon' 오브젝트를 확인 할 수 있을 것이다.
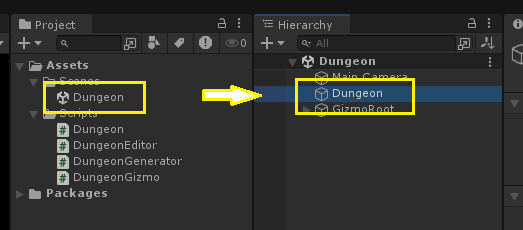
Dungeon 오브젝트를 클릭하면 Inspector 창에서 랜덤 던전의 생성 과정을 테스트 해볼 수 있는 버튼들이 나타난다. 이 버튼들을 순서대로 클릭해 어떤 식으로 던전이 생성되는지 확인해 볼 수 있다.