삼각형의 외접원 구하기

들어가며

점 세 개로 이루어진 다각형을 우리는 삼각형이라고 부르고, 이 삼각형의 모든 꼭지점을 지나는 원을 '삼각형의 외접원'이라고 정의 한다.

만일 여러분이 직접 컴퍼스를 들고 삼각형의 세 꼭지점이 동시에 놓이는 원을 그리려고 하면 '모든 점을 지나는 원'의 '중심'을 정확히 찾기가 쉽지 않다는 것을 알게 될 것이다.

하지만 원리만 안다면 그렇게 어렵지 않게 삼각형의 외접원을 구하는 것이 가능하다. 이번 포스트에는 외접원을 구하는 원리에 대해 살펴 보도록 하겠다.

원의 정의

기하학에서 원(圓, 영어: circle)은 '평면 위의 한 점으로 부터 일정한 거리에 있는 점들의 집합'으로 정의 되고 있다. 좀 더 간단히 말하면 원은 '중심점'과 '반지름'으로 구성되어 있다는 말이다.

원은 중심점과 반지름을 이용해 그릴 수 있다

삼각형의 외접원을 그리기 위해서는 외접원의 중심점의 위치와 반지름을 알아야 한다. 이번 포스트를 통해 우리는 삼각형의 세 꼭지점을 이용해 원의 중심점과 반지름을 구하는 방법에 대해 살펴 볼 것이다.

삼각형의 외심

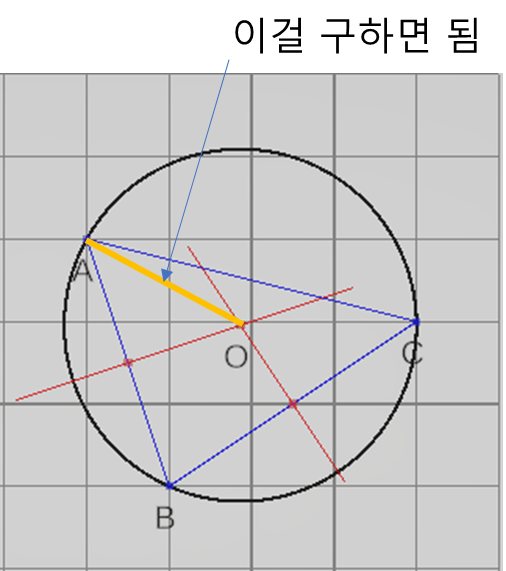
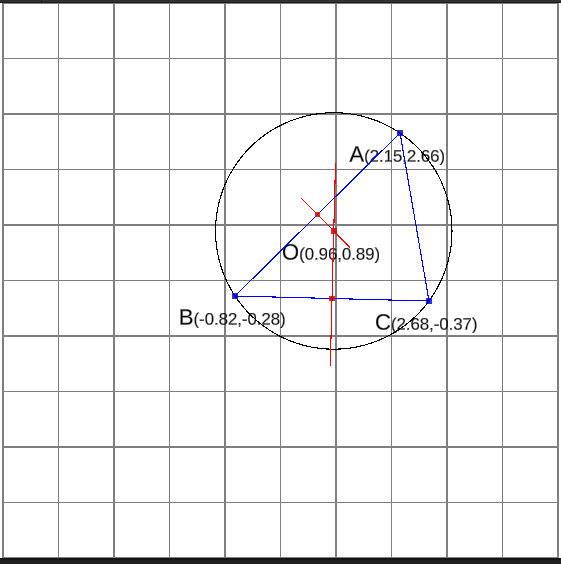
먼저 원의 중심점에 대해 이야기 해보도록 하겠다. 아래 그림에서 여러분은 삼각형의 각 꼭지점을 지나는 '삼각형의 외접원'과 그 원의 가운데 찍혀 있는 점 O를 확인 할 수 있다. 이 '삼각형의 외접원'의 중심을 '삼각형'의 '외심'이라고 한다.

외심의 특징

위 그림에서 우리는 외심의 중요한 특징을 찾을 수 있다.

외심에서 각 꼭지점 까지의 길이는 모두 같다.

외심은 원의 중심이고, 그 원은 모든 꼭지점을 지나고 있다. 이것은 모든 꼭지점들은 '외심'으로 부터 원의 반지름 만큼 떨어져 있다는 뜻이다.

위 그림 처럼 원의 중심으로 부터 각 꼭지점들을 빨간색 선으로 연결하면 세 개의 이등변 삼각형들을 얻을 수 있다.

외심 O에서 각 꼭지점 A, B, C에 이르는 길이는 같다.
두 변의 길이가 같은 삼각형을 이등변 삼각형이라고 한다.

이등변 삼각형의 특징은 꼭지각에서 밑변으로 수선을 그으면 밑변의 이등분 점에 도착한다는 것이다.

정리하면 :

삼각형의 '외심'으로 부터 삼각형의 각 꼭지점까지의 길이는 같으므로 이것을 이용해 이등변 삼각형 AOB, BOC, COA 세 개를 구할 수 있다.
이등변 삼각형의 꼭지각으로 부터 밑변에 수직하는 직선을 그었을 때 닿는 점은 밑변을 이등분하는 위치다.

앞에서 정리한 내용을 거꾸로 생각하면 다음과 같이 삼각형의 각 꼭지점으로 부터 외심의 위치를 찾아 낼 수 있다 :

삼각형의 각 꼭지점 A, B, C를 알고 있고, 각 꼭지점을 연결해 삼각형의 세 변을 구할 수 있다.
이 변들은 이등변 삼각형의 밑변이 된다.
앞에서 구한 삼각형의 세 변들의 중심에 각각 수직하는 직선들을 구한다.
앞에서 구한 수직하는 직선들의 교점이 이 삼각형의 외심이 된다.

삼각형 각 변의 중점에 수직하는 직선들 끼리 만나는 점이 외접원의 중심. 즉, '외심'이 된다.

위 그림은 직선 AB와 직선 BC에 각각 수직인 두 직선의 교점 O가 삼각형 ABC의 외심 위치라는 것을 보여주고 있다.

외심 구하기

앞서 살펴본 개념들을 통해 외심의 위치를 찾을 수 있는 공식을 만들어 보도록 하겠다.

1. 삼각형의 꼭지점으로 부터 두 변의 수직이등분선을 구한다

삼각형의 각 변으로 부터 수직이등분선의 방정식을 구해보자. 그럼 세 변에 대해서 모두 구해야 하나? 아니 그럴 필요는 없다. 두 직선의 교점이든 세 직선의 교점이든 교점의 위치는 하나다. 우리는 직선 AB, BC 두 직선의 수직이등분선을 구하도록 하겠다.

직선 AB에 수직인 직선의 기울기

먼저 직선 AB의 기울기를 구해야 한다. 직선의 기울기는 'y축의 증가 값 나누기 x축의 증가 값'으로 정의 된다. 증가 값은 현재 값에서 이전 값을 빼주면 된다. 여기서는 A를 이전 값, B를 현재 값이라고 정의하겠다.

그럼 (B.y - A.y) / (B.x - A.x)가 직선 AB의 기울기다. 하지만 우리가 필요한 것은 직선 AB의 기울기가 아니라 이 직선을 수직으로 지나가는 직선이 필요하다.

직선에 수직인 기울기를 가진 직선의 조건은 '두 기울기를 곱했을 때 결과가 -1'이어야 한다.

원래 직선의 기울기 * 수직인 직선의 기울기 = -1

따라서 :

(B.y - A.y) / (B.x - A.x) * 수직인 기울기 = -1

'수직 기울기' 를 구하기 위해 위 방정식의 양 변에 1/( (B.y - A.y) / (B.x - A.x) )을 곱해 주면 아래와 같은 공식을 구할 수 있다.

직선 AB에 수직인 직선의 기울기 = (B.x - A.x) / (B.y - A.y) * -1

이렇게 직선 AB에 직교하는 직선의 기울기를 구했다. 이것을 이제 부터 m_ab라고 부르도록 하겠다.

직선 AB의 수직이등분선 구하기

앞에서 우리는 직선 AB에 수직인 직선의 기울기를 구했다. 하지만 우리가 필요한 것은 기울기 뿐만 아니라 직선 AB의 중심을 지나는 직선이다. 직선의 중심을 좌표는 두 좌표를 더해 나누기 2를 하는것으로 간단히 구할 수 있다. (x축의 중심 좌표는 a₁, y축의 중심 좌표는 b₁이라고 부르도록 하겠다)

a₁ = (A.x + B.x) / 2 <- x 축 중심 좌표
b₁ = (A.y + B.y) / 2 <- y 축 중심 좌표

이제 우리에게 필요한 모든 것은 다 갖추었다. 우리는 직선의 기울기m_ab를 구했으며, 이 직선이 좌표 (a₁, b₁)를 지나야 한다는 것을 알고 있다. 이를 가지고 직선의 방정식을 다시 만들면 :

m_ab = (y - b₁) / (x - a₁) <- y 증가 값 나누기 x 증가 값. 기울기 공식
y - b₁ = m_ab(x - a₁)
y = m_ab(x - a₁) + b_{1 <- 직선 AB에 수직이등분 직선의 방정식}

위와 같은 방정식을 얻을 수 있다.

직선 BC의 수직이등분선 구하기

직선 AB의 중심을 지나는 수직이등분선을 구했으니 이제 직선 BC를 지나는 수직이등분선을 구할 차례다. 앞에서 직선 AB의 수직이등분선을 구했던 것과 같은 과정을 거치면 직선 BC의 수직이등분선 방정식도 구할 수 있다. 앞으로 직선 BC의 수직 기울기는 m_bc,중점 좌표는 (a₂, b₂)라고 정의하도록 하겠다.

y = m_bc(x - a₂) + b₂

2. 두 수직이등분선의 교점을 구한다

앞에서 구한 두 수직이등분선의 방정식은 아래와 같다.

첫 번째 직선: y₁ = m_ab(x₁ − a₁) + b₁
두 번째 직선: y₂ = m_bc(x₂ − a₂) + b₂

이를 좌표계를 동일하게 하기 위해 x₁과 x₂를 그냥 x로 두고, y₁과 y₂를 y로 두도록 한다. 즉,

y = m_ab(x - a₁) + b₁
y = m_bc(x - a₂) + b₂

라는 두 방정식을 얻을 수 있다. 이제 두 방정식을 비교하여 교점 x의 값을 찾아보자. 교점이라는 것은 결국 x 축과 y 축의 값이 같다는 뜻이다. 그래서 y 값이 같다고 가정하고 두 방정식을 다음과 같이 세울 수 있다.

m_ab(x - a₁) + b₁ = m_bc(x - a₂) + b₂

이를 정리하면

m_abx - m_aba₁ + b₁ = m_bcx - m_bca₂ + b_{2 <- 두 방정식 모두 같은 y 값을 가지고 있다고 가정}
m_abx - m_bcx = m_aba₁ - b₁ - m_bca₂ + b₂ <- x 값을 구하기 위해 한쪽으로 이항
x(m_ab - m_bc) = m_aba₁ - m_bca₂ - b₁ + b₂

x = (m_aba₁ - m_bca₂ - b₁ + b₂) / (m_ab - m_bc)

위의 식에서 얻어지는 x 값이 두 직선이 교차하는 x 좌표가 된다.

※ 단, 위의 식에서 m_ab와 m_bc의 값은 같지 않아야 한다. 기울기가 같다는 것은 평행하거나 동일한 직선이라는 의미고 그것은 교차할 수 없다는 뜻이므로, 만일 m_ab와 m_bc가 같다면 교차점을 찾을 수 없다.

이제 y 좌표를 구하기 위해 위에서 구한 x 값을 직선 AB의 수직이등분선을 구하는 방정식에 대입해 보자(물론 BC의 수직이등분선의 방정식에 대입해도 된다).

y = m_ab(x - a₁) + b₁

최종적으로 두 직선의 교점을 구하는 방정식은 다음과 같이 구할 수 있다.

x = (m_aba₁ - m_bca₂ - b₁ + b₂) / (m_ab - m_bc)
y = m_ab( (m_aba₁ - m_bca₂ - b₁ + b₂) / (m_ab - m_bc) - a₁) + b₁

하지만 x는 바로 위에서 구했으므로 더 간단하게 'y = m_ab(x - a₁) + b₁'로 정리할 수 있다.

특수한 경우

수직이등분선의 기울기가 0인 경우(수평선)

직선의 방정식이 'y = m(x - a) + b'이고 기울기 m이 0일 때, 방정식은 다음과 같이 단순화 된다.

y = b

이는 수평선이며, x 값이 무엇이든, 모든 x좌표에 대해 y는 항상 b이다.

이제 이 수평선 y = b와 다른 직선의 교점을 구하려면, 다른 직선의 방정식이 주어져야 한다. 예를 들어 y = m'(x - a') + b' 형태라면 주어진 수평선 y = b와의 교점을 구하는 과정은 다음과 같다.

첫 번째 직선 : y = b (수평선)
두 번째 직선 : y = m'(x - a') + b'

두 직선의 교점을 구하기 위해 연립 방정식을 세워 보자. y는 b와 같으므로 아래와 같은 연립 방정식이 세워진다.

b = m'(x - a') + b

위 식을 정리하면 :

b - b' = m'(x - a')
(x - a') = (b - b') / m'

x = a' + (b - b') / m' <- 최종 방정식

x의 값은 위 방정식으로 구할 수 있고, y는 b와 같으므로 수평선과 다른 직선의 교점 좌표는 다음과 같다.

x = a' + (b - b') / m'
y = b

※ 만일 m' = 0. 즉, 두 번째 직선도 수평선이라면 같다면 평행하거나 겹치므로 교점이 하나도 없거나 무수히 많은 교점이 있으므로 교점을 구할 수 없다.

수직이등분선의 기울기가 무한인 경우(수직선)

직선의 방정식이 'y = m(x - a) + b'이고 기울기 m이 무한이라면, 이는 수직선을 나타낸다. 수직선은 x가 일정한 값을 가지며, 방정식은 다음과 같이 표현된다.

x = a

이제 이 수직선 x = a와 다른 직선의 교점을 구해 보겠다. 다른 직선의 방정식이 y = m'(x - a') + b' 형태라면, x에 a를 대입하여 교점을 구한다.

y = m'(a - a') + b'

따라서 교점의 좌표는 다음과 같다 :

x = a
y = m'(a - a') + b'

※ m' = 0. 즉, 다른 직선이 수평선인 y = b'일 경우, 수직선 x = a에서의 y좌표는 b'이다.

x = a
y = b'

외접원의 반지름 구하기

이제 원의 두 구성 요소 중 남은것은 원의 반지름이다.
앞에서 우리는 두 수직이등분선의 교점, 즉 삼각형의 '외심'의 좌표를 구했다. 이제 원의 반지름은 삼각형의 외심으로 부터 삼각형의 한 꼭지점까지의 길이를 구하면 된다.

두 점 사이의 길이를 구하는 공식은 다음과 같다.

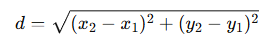
※ 어떻게 위 공식이 나왔는지 궁금하다면 [여기]를 참고 하도록하자.
위 공식을 통해 직선 AO의 길이를 구하면 외접원의 반지름을 구할 수 있다.

마치며

마침내 우리는 외접원의 중심점과 반지름을 구할 수 있게 되었다. 지금까지 살펴 보았던 내용들을 요약하면 다음과 같다 :

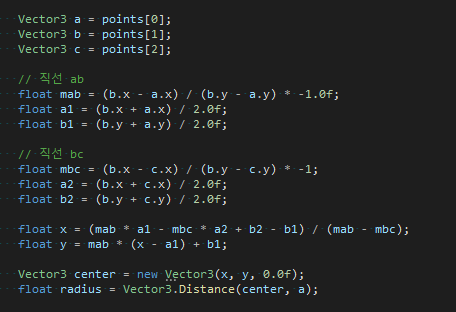
직선 AB의 수직 기울기 : m_ab = (b.x - a.x) / (b.y - a.y) * -1
직선 AB의 x축 중심점 : a₁ = (b.x + a.x) / 2
직선 AB의 y축 중심점 : b₁ = (b.y + a.y) / 2
직선 BC의 수직 기울기 : m_bc = (b.x - c.x) / (b.y - c.y) * -1
직선 BC의 x축 중심점 : a₂ = (b.x + c.x) / 2
직선 BC의 y축 중심점 : b₂ = (b.y + c.y) / 2
외접원의 x축 중심점 : x = (m_ab * a₁ - m_bc * a₂ + b₂ - b₁) / (m_ab - m_bc)
외접원의 y축 중심점 : y = m_ab * (x - a₁) + b₁
외접원의 반지름 : r = sqrt((x - a.x) * (x - a.x) + (y - a.y) * (y - a.y))
※ sqrt( ... )는 루트 연산을 의미한다.

본 포스트에 사용된 외접원의 이미지는 유니티(2021.3.9f1)를 이용해 생성되었으며, 해당 프로젝트는 [여기]에서 확인 할 수 있다. 유니티에서 해당 프로젝트를 실행 후 CircumCircle 씬을 실행하면 아래와 같이 점 세 개를 찍으면 외접원을 그려주는 화면을 볼 수 있다.

프로젝트 내부에 이런저런 코드들이 많이 있지만 대부분 그림을 그리기 위한 것들이고 실제 외접원을 계산하는 코드 부분은 아래가 전부다.

이상 삼각형의 외접원에 대해 살펴 보았다. 원래는 랜덤 생성 맵을 만들고 있었는데 맵을 제대로 만드려면 들로네 삼각분할(Delaunay Triangulation)이라는 것이 필요했고, 들로네 삼각분할을 구현하려면 삼각형의 외접원을 구할수 있어야 했다. 그렇게 필요한 것들을 찾아 공부하다보니 여기까지 오게 되었다.
다음 포스트는 들로네 삼각분할(Delaunay Triangulation)분할에 대해 다뤄 보도록 하겠다.

부록 1. 같이 읽으면 좋은 글

저작자표시 비영리

HardCore in Programming

삼각형의 외접원 구하기

들어가며

원의 정의